Divkāršais integrālis

Divkāršais integrālis ir noteiktā integrāļa vispārinājums, kad integrēšanas apgabals D ir plaknes apgabals, bet zemintegrāļa funkcija ir divu argumentu funkcija z = f(x, y). Divkāršo integrāli apzīmē ar simbolu $\underset{(D)}{\iint }f(x,y)dS.$

Ja $f(x,y)⩾0$, divkāršajam integrālim ir noteikta ģeometriskā interpretācija: tas vienāds ar tāda ķermeņa tilpumu V, ko ierobežo funkcijas z = f(x, y) grafiks (tas ir, virsma ar vienādojumu z = f(x, y)), xy plaknes apgabals (D) un cilindriska virsma ar veidotājām paralēlām Oz asij, kas iet caur apgabala (D) robežlīniju. Tātad

$\underset{(D)}{\iint }f(x,y)dS=V.$

Definīcija

Pieņem, ka funkcija z = f(x, y) ir definēta Oxy apgabalā (D):

1. Ar brīvi izraudzītām līnijām apgabalu (D) sadala n daļās (D₁), (D₂), (D₃), ..., (D_i), ..., (D_n). Šo daļu laukumus apzīmē ar $△S_1,△S_2,△S_3,...,△S_i,...,△S_n.$
2. Katrā apgabala daļā (D_i) brīvi izraugās punktu $M_i({\xi }_i;{\eta }_i)\in (D_i)$, $1⩽i⩽n$.
3. Aprēķina funkcijas z = f(x, y) vērtības izraudzītajos punktos, tas ir, atrod $f(M_i)=f({\xi }_i;{\eta }_i)$, $1⩽i⩽n$.
4. Atrastās funkcijas vērtības $f({\xi }_i;{\eta }_i)$reizina ar tās apgabala daļas (D_i) laukumu $△S_i$, kurā atrodas punkts $M_i$, tas ir, aprēķina$f({\xi }_i;{\eta }_i)$$△S_i$, $1⩽i⩽n$.
5. Aprēķina visu reizinājumu $f({\xi }_i;{\eta }_i)$$△S_i$ summu $\sum _{i=1}^{n}f({\xi }_i;{\eta }_i)△S_i.$ Šo izteiksmi sauc par funkcijas z = f(x, y) integrālsummu apgabalā (D).
6. Aprēķina integrālsummas robežu, kad maksimālais apgabala daļas (D_i) diametrs d_i tiecas uz 0 (par daļas (D_i) diametru sauc taisnes nogriezni, kas savieno divus vistālākos (D_i) robežlīnijas punktus), tas ir aprēķina $\underset{d\to 0}{\lim }\sum _{i=1}^{n}f({\xi }_i;{\eta }_i)△S_i.$

Ja šī robeža eksistē neatkarīgi no dalījuma veida daļās un no punktu izvēles katrā daļā, tad šo robežu sauc par funkcijas z = f(x, y) divkāršo integrāli apgabalā (D) un apzīmē ar simbolu $\underset{(D)}{\iint }f(x,y)dS$ vai $\underset{(D)}{\iint }f(x,y)dxdy.$

Tādējādi $\underset{d\to 0}{\lim }\sum _{i=1}^{n}f({\xi }_i;{\eta }_i)△S_i=\underset{(D)}{\iint }f(x,y)dS.$

Ja funkcija z = f(x, y) apgabalā (D) ir nepārtraukta vai gabaliem pārtraukta, tad šai funkcijai eksistē divkāršais integrālis.

Īpašības

1. īpašība

Divkāršais integrālis no funkcijas summas (starpības) ir vienāds ar doto funkciju integrāļu summu (starpību):

$\underset{(D)}{\iint }(f_1(x,y)+f_1(x,y))dxdy=\underset{(D)}{\int }{f}_1(x,y)dxdy+\underset{(D)}{\int }{f}_2(x,y)dxdy+...+\underset{(D)}{\int }{f}_n(x,y)dxdy.$

2. īpašība

Konstantu reizinātāju C var ņemt pirms integrāļa zīmes:

$\underset{(D)}{\iint }Cf(x,y)dxdy=C\underset{(D)}{\iint }f(x,y)dxdy.$

3. īpašība — Aditivitātes īpašība

Ja apgabals (D) sadalīts vairākās daļās, tad integrē pa katru daļu atsevišķi un iegūtos rezultātus saskaita:

$\underset{(D)}{\iint }f(x,y)dxdy=\underset{(D_1)}{\int }f(x,y)dxdy+\underset{(D_2)}{\int }f(x,y)dxdy+...+\underset{(D_n)}{\int }f(x,y)dxdy.$

4. īpašība

Ja apgabalā (D) funkcija saglabā zīmi $f(x,y)⩾0$ $(⩽0)$, tad divkāršajam integrālim ir tāda pati zīme:

$\underset{(D)}{\iint }f(x,y)dxdy⩾0$ $(⩽0).$

5. īpašība

Ja apgabalā (D) visiem (x, y) izpildās nevienādība $f(x,y)⩽g(x,y)$, tad arī divkāršajiem integrāļiem izpildās šāda nevienādība:

$\underset{(D)}{\iint }f(x,y)dxdy⩽\underset{(D)}{\iint }g(x,y)dxdy.$

6. īpašība — Divkāršā integrāļa novērtējums

Ja funkcijai z = f(x, y) slēgtā apgabalā (D) ir nepārtraukta un m ir funkcijas z = f(x, y) vismazākā vērtība, bet M ir funkcijas z = f(x, y) vislielākā vērtība apgabalā (D), tas ir, $m⩽f(x,y)⩽M$ , tad izpildās nevienādības:

$mS⩽\underset{(D)}{\iint }g(x,y)dxdy⩽MS,$

kur S ir apgabala (D) laukums.

7. īpašība — Vidējās vērtības teorēma

Ja funkcija z = f(x, y) slēgtā apgabalā (D) ir nepārtraukta, tad apgabalā (D) eksistē vismaz viens tāds punkts P, ka divkāršais integrālis pa apgabalu (D) ir vienāds ar zemintegrāļa funkcijas vērtību šajā punktā, reizinātu ar apgabala (D) laukumu S:

$\underset{(D)}{\iint }f(x,y)dxdy=f(P)\cdot S.$

Funkcijas z = f(x, y) vērtību $f(P)$ sauc par funkcijas integrālo vidējo vērtību apgabalā (D).

Aprēķināšana Dekarta koordinātās

• 
  Attēlots apgabals (D) regulārs Oy ass virzienā.
• 
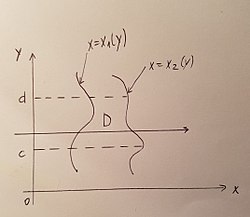
  Attēlots apgabals (D) regulārs Ox ass virzienā.

Apgabalu (D) sauc par regulāru Oy ass virzienā, ja jebkura taisne, kas paralēla Oy asij, šī apgabala robežu krusto ne vairāk kā divos

punktos.

Apgabalu (D) sauc par regulāru Ox ass virzienā, ja jebkura taisne, kas paralēla Ox asij, šī apgabala robežu krusto ne vairāk kā divos punktos.

Divkāršo integrāli Dekarta koordinātu sistēmā reducē uz atkārtotiem integrāļiem. Tos var pierakstīt divos veidos pēc tā, kādā virzienā apgabals (D) ir pareizs:

$I_1=\underset{a}{\overset{b}{\int }}dx\underset{y_1(x)}{\overset{y_2(x)}{\int }}f(x,y)dy$ (regulārs Oy ass virzienā)

un

$I_2=\underset{c}{\overset{d}{\int }}dy\underset{x_1(y)}{\overset{x_2(y)}{\int }}f(x,y)dx$ (regulārs Ox ass virzienā).

Ārējās integrāļa robežas vienmēr ir konstantas.

Ja apgabals nav pareizs ne Oy, ne Ox ass virzienā, tad apgabalu (D) sadala atsevišķā daļās, integrē pa katru daļu atsevišķi un iegūtos rezultātus saskaita.

Atkārtotos integrāļus aprēķina šādi:

$I_1=\underset{a}{\overset{b}{\int }}dx\underset{y_1(x)}{\overset{y_2(x)}{\int }}f(x,y)dy=\underset{a}{\overset{b}{\int }}(\underset{y_1(x)}{\overset{y_2(x)}{\int }}f(x,y)dy)dx=\underset{a}{\overset{b}{\int }}{F}_1(x,y){|}_{y=y_1(x)}^{y=y_2(x)}dx=\underset{a}{\overset{b}{\int }}(F_1(x,y_2(x))-F_1(x,y_1(x)))dx={\varphi }_1(x){|}_a^b={\varphi }_1(b)-{\varphi }_1(a)=K_1$ (iekšējo integrāli rēķina pēc y, bet mainīgo x uzskata par konstanti)

un$I_2=\underset{c}{\overset{d}{\int }}dy\underset{x_1(y)}{\overset{x_2(y)}{\int }}f(x,y)dx=\underset{c}{\overset{d}{\int }}(\underset{x_1(y)}{\overset{x_2(y)}{\int }}f(x,y)dx)dy=\underset{c}{\overset{d}{\int }}{F}_2(x,y){|}_{x=x_1(y)}^{x=x_2(y)}dy=\underset{c}{\overset{d}{\int }}(F_2(x_2(y),y)-F_2(x_1(y))dx={\varphi }_2(y){|}_c^d={\varphi }_2(d)-{\varphi }_2(c)=K_2$

(iekšējo integrāli rēķina pēc x, bet mainīgo y uzskata par konstanti).

Jaunu mainīgo ieviešana

Divkāršā integrāļa aprēķināšanu var vienkāršot, ieviešot jaunus mainīgos (u, v) ar formulām:

$\{\begin{array}{c}x=x(u,v);\\ y=y(u,v).\end{array}$

Iegūst:

$\underset{(D)}{\iint }f(x,y)dxdy=\underset{(D)}{\iint }f(x(u,v),y(u,v))|J(u,v)|dudv,$

kur $J(u,v)$ ir Jakobi determinants jeb jakobiāns:

$J(u,v)=\left|\begin{array}{cc}\frac{\partial x}{\partial u}& \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u}& \frac{\partial y}{\partial v}\end{array}\right|.$

Aprēķināšana polārajās koordinātās

Polārās un Dekarta koordinātas

Ja integrācijas apgabalu (D) ierobežo riņķa līnijas vai arī līniju vienādojumi un zemintegrāļa izteiksme satur kvadrātu summu $x^2+y^2$, aprēķinus var vienkāršot, pārejot uz polārajām koordinātām $(\phi ,r)$, izmantojot formulas:

$\{\begin{array}{c}x=rcos\phi ;\\ y=rsin\phi .\end{array}⟹x^2+y^2=r^2$

Jakobiānu aprēķina pēc formulas:

$J(u,v)=\left|\begin{array}{cc}\frac{\partial x}{\partial u}& \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u}& \frac{\partial y}{\partial v}\end{array}\right|=\left|\begin{array}{cc}cos\phi & -rsin\phi \\ sin\phi & rcos\phi \end{array}\right|=r.$

Iegūst pārejas formulu no Dekarta uz polārajām koordinātām:

$\underset{(D)}{\iint }f(x,y)dxdy=\underset{(D)}{\iint }f(rcos\phi ,rsin\phi )rdrd\phi .$

Ja plaknes apgabalu ierobežo stari $\phi =\alpha ;\phi =\beta$ un līnijas $r=r_1(\phi );r=r_2(\phi )$, iegūst:

$\underset{(D)}{\iint }f(x,y)dxdy=\underset{\alpha }{\overset{\beta }{\int }}d\phi \underset{r_1(\phi )}{\overset{r_2(\phi )}{\int }}f(rcos\phi ,rsin\phi )rdr.$

Pielietojumi

Plaknes figūras laukuma aprēķināšana

Ja zemintegrāļa funkcija $f(x,y)=1$, tad divkāršais integrālis ir vienāds ar integrēšanas apgabala (D) laukumu Dekarta un polārajās koordinātās:

$S=\underset{(D)}{\iint }dS=\underset{(D)}{\iint }dxdy=\underset{(D)}{\iint }rdrd\phi .$

Tilpuma aprēķināšana

Ķermeni ierobežo funkcijas $z=f_1(x,y),z=f_2(x,y)$.

Ja ķermeni ierobežo funkcijas $z=f(x,y)$grafiks, kur $f(x,y)⩾0$, Oxy plakne un Oz asij paralēla cilindriska virsma, kas iet caur apgabala (D) robežlīniju. Šāda ķermeņa tilpums ir vienāds ar

$V=\underset{(D)}{\iint }f(x,y)dxdy.$

Ja ķermeni ierobežo Oz asij paralēla cilindriska virsma, kas iet caur apgabala (D) robežlīniju un divu funkciju $z=f_1(x,y),z=f_2(x,y)$ grafiki, turklāt $0⩽f_1(x,y)⩽f_2(x,y)$, tad ķermeņa tilpums ir

$V=\underset{(D)}{\iint }(f_2(x,y)-f_1(x,y))dxdy.$

Virsmas laukuma aprēķināšana

Ja dota virsma $z=f(x,y)$, kur funkcija $z=f(x,y)$ ir nepārtraukta apgabalā (D) — virsmas $z=f(x,y)$ projekcija Oxy plaknē — un tai eksistē nepārtraukti parciālie atvasinājumi $z{\text{'}}_x$ un $z{\text{'}}_y$. Šīs virsmas laukumu var aprēķināt ar formulu

$S=\underset{(D)}{\iint }\sqrt{1+(z{\text{'}}_x{)}^2+(z{\text{'}}_y{)}^2}dxdy.$

Nehomogēnas plakanas plāksnītes masas aprēķināšana

Ja nepārtraukta funkcija $\rho (x,y)$ ir nehomogēnas plakanas plāksnītes (D) virsmas blīvuma sadalījums, tad plāksnītes masa ir

$m=\underset{(D)}{\iint }\rho (x,y)dxdy.$